A coffee filter for pharmaceuticals?

To recover a freshly made pharmaceutical from its liquid reaction mixture, the mixture is often boiled, requiring a lot of energy. But what if we could recover such a drug using a simple filter? And how do we select a good filter for the wide range of solvents and drugs used and produced? In our recent article, we show that is important to consider how much the drug likes to be dissolved in the solvent, to select a good membrane filter.

A coffee filter for small molecules

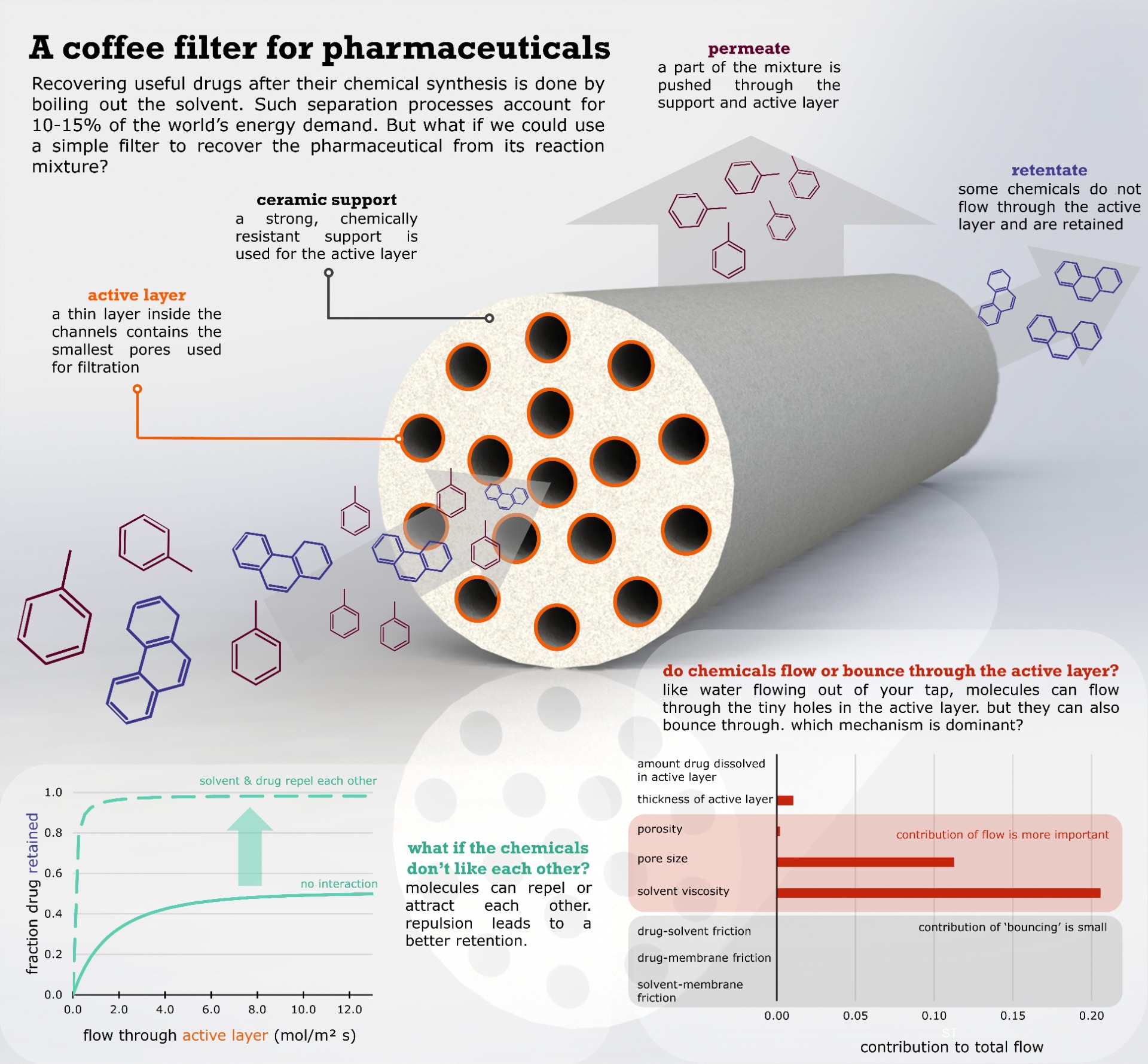
Pushing a solvent mixture through a filter with extremely tiny pores is proving to be a good alternative to just boiling out the solvent. The method is also called organic solvent nanofiltration or organic solvent reverse osmosis. Especially ceramic membranes are very promising: they contain very small pores, are highly resistant to abrasive solvents and they can be modified chemically to finetune their selectivity.

How do you select a good membrane filter?

But how do you know which kind of membrane you should use? Different ceramic membranes contain different sizes of pores and might block different solvents or pharmaceuticals. Chemical modifications can also change which drug or solvent is retained and which not. One option could be to look at the size of a molecule: you would expect larger molecules to be more easily filtered out. Experiments have surprisingly shown the opposite. Different molecules of the same size can be either completely blocked or can completely pass through. To test different filters for a given application can be tedious, costly and time consuming.

Do chemicals flow or bounce through?

We develop mathematical models which can help us predict which membrane might work for a given separation problem. A computer could thus help us decide which membrane to use. Such models also give insights into which mechanisms are important when our mixture of solvent and pharmaceutical is flowing through the membrane pores. In our recent work, we investigated transport through membrane pores using the Maxwell-Stefan equations. A relatively complicated theory, this model considers most of the important effects at play.

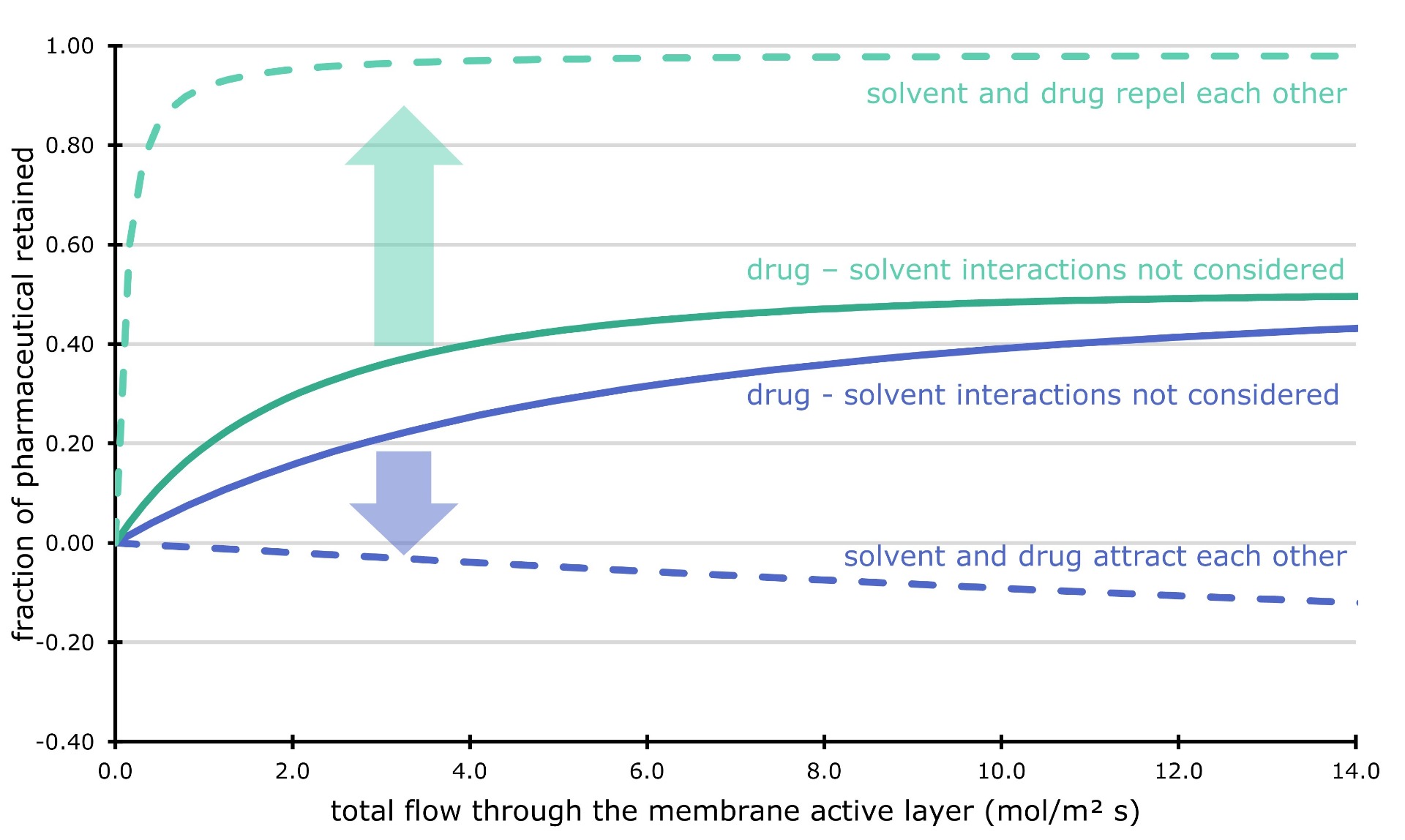
As a first result, we showed that interactions between the solvent and the pharmaceutical drug are important to consider. We took a pharmaceutical component and calculated how much it likes to be dissolved in different solvents. Next, we simulated the filtration through the fine pores of a ceramic membrane. We assumed that the pharmaceutical dissolved in the same way into the membrane pores, independent of the liquid solvent. Surprisingly, we could show that the membrane filter would completely block the pharmaceutical component when it is dissolved in a solvent it likes. On the other hand, if we use a 'bad' solvent, the membrane filter would not work. The drug would just flow through with the solvent.

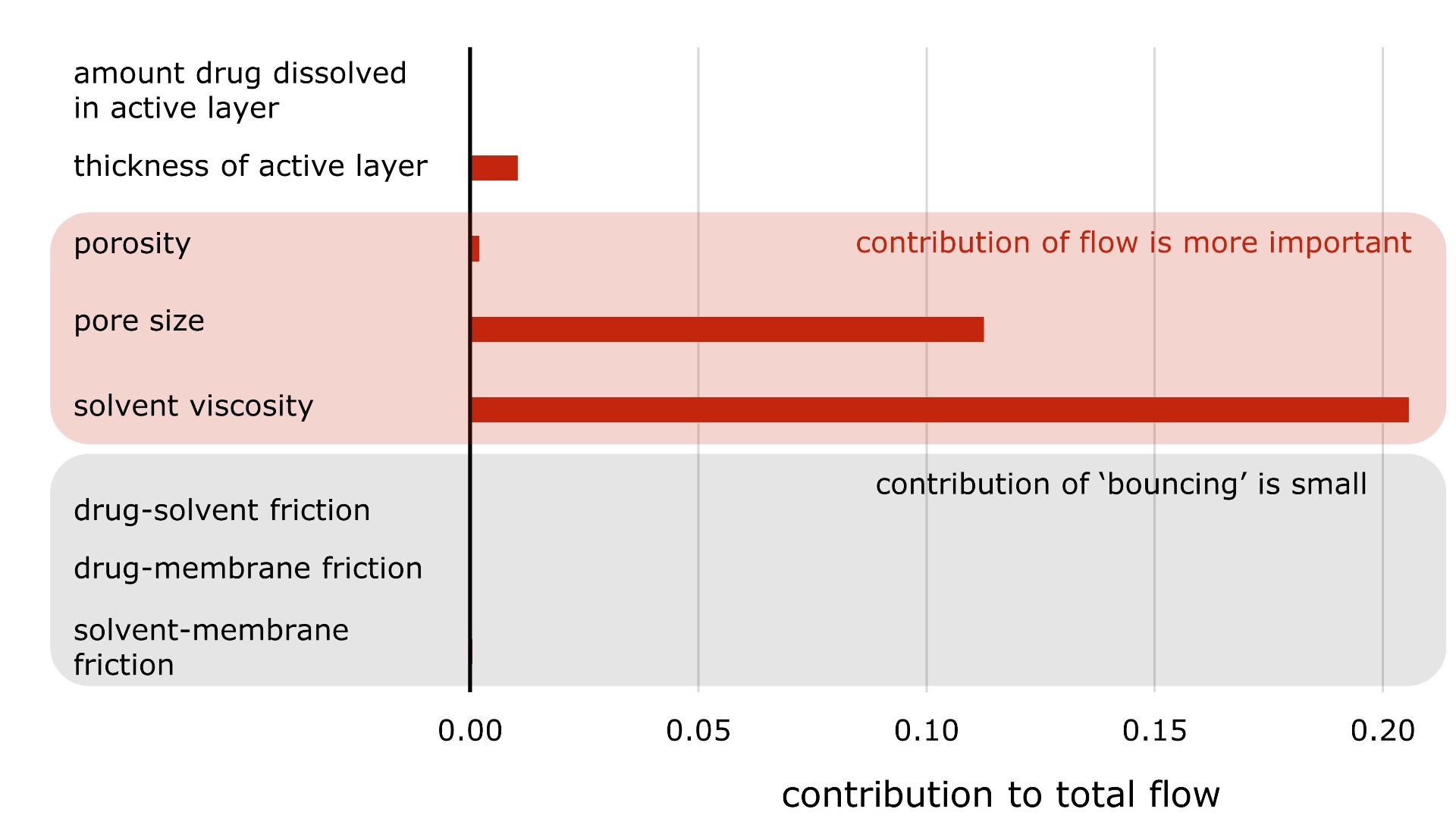
Secondly, we observed that Maxwell-Stefan theory predicts the flow through the tiny membrane pores to be 'viscous' for most pore sizes. Two different mechanisms contribute when molecules flow through such tiny holes. Firstly, chemicals randomly bounce with each other and with the walls. This is called diffusion. A second mechanism is the same one which happens when you open your tap to fill a glass of water - liquid flows through bulk motion. In the range of pore sizes we considered, bulk flow appears to be the most important.

Our work thus shows that we need to consider pharmaceutical-solvent interactions if we want to move towards computer-aided membrane selection. Secondly, by identifying the most important transport mechanisms, we can simplify our mathematical models. This opens perspectives to implement a simpler model in a process simulator, allowing for digital process design or control.